Home
Mission
Overview of Project
Project Staff
Sponsors
Achievements
Checking, Illustrations
Upcoming Activities
Id and Species Lists
Protea Information
Protea Gallery
Growing Proteas
Interim Dist. Maps
Publications
Afrikaanse Inligting
The Fibonacci Sequence
Fibonacci (1170-1230) introduced Arabic numerals to Europe. Being a mathematician, he attempted to solve a problem which he had raised: How big would a rabbit colony be each month if rabbits gave birth to a pair of young every month and started breeding at two months of age? The solution he discovered was to add the rabbits from the previous month with the young from the current month. This gives a sequence (the Fibonacci sequence) in which "each number is the sum of the two preceding numbers". Thus, the sequence progresses: 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 ... The growth rate of successive numbers gives a ratio which converges on 1/2X(1+/5) = 1.618 which is the "divine proportion" or "golden section" of geometry and aesthetics. But that does not concern us here.
More importantly Fibonacci numbers are found in
the arrangement of leaves (phyllotaxis). Leaves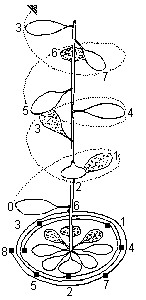 
do not occur
at random on a stem: they may be arranged as alternative,
opposite, whorled, or, as in proteas, spirally. Looking at the
figure opposite (of King Sugarbush - Protea cynaroides), we see that every eighth leaf occupies the same
vertical position on the stem. Furthermore, every eighth leaf
occurs at exactly three turns: i.e. there are three windings (or
turns) per period. Call the number of leaves per period n
and the number of turns per period m and P. cynaroides has
m = 3 and n = 8: two Fibonacci numbers! In fact, cabbages, asters
and hawkweed share this same m and n. Many bulbous
plants have m = 1, n = 2, sedges, alders and birches have m = 1,
n = 3, whereas m =2, n = 5 occurs in willows, roses and
stone-fruit trees; m = 8, n = 21 occurs in spruce and fir cones;
and m = 13, n = 34 occurs in some pines. Always Fibonacci numbers
- no, not always - but usually.
This raises several interesting questions. Do all Proteaceae have the m = 3, n = 8 Fibonacci numbers for their leaves? And if seedheads are also based on m = 3, n = 8, should not the number of fruit per head be multiples of these two numbers?
But we are not
yet finished with Fibonacci numbers. The number of ray florets
per head for species of alpine daises equals a Fibonacci number,
although individual heads may bear a few more or less florets.
Again, a few exceptions occur, but not many. What about proteas?
The illustration opposite has 55 outer spirals clockwise and 34
spirals in a counter-clockwise direction at the outer edge! If we
count the number of seeds per spiral inwards we get roughly: 59
59 57 56 55 54 50 34 34 34 24 (20, 12 -the two inner whorls are
impossible to determine): more or less Fibonacci numbers. But the
ca 548 seeds per head is not a Fibonacci number: in fact
only Protea species with fewer than 100 seeds per head even
approach Fibonacci numbers.
But what does this all mean? Why are Fibonacci numbers so prevalent in plants? The answer must have to do with symmetry: How does one arrange the leaves on a stem (or the seeds in a head) in such a way so as to simultaneously keep: the plumbing (xylem and phloem vessels) simple; the orientation suitable to ensure exposure to light (leaves) or tightest packing (seeds); and the mechanical support rigid.
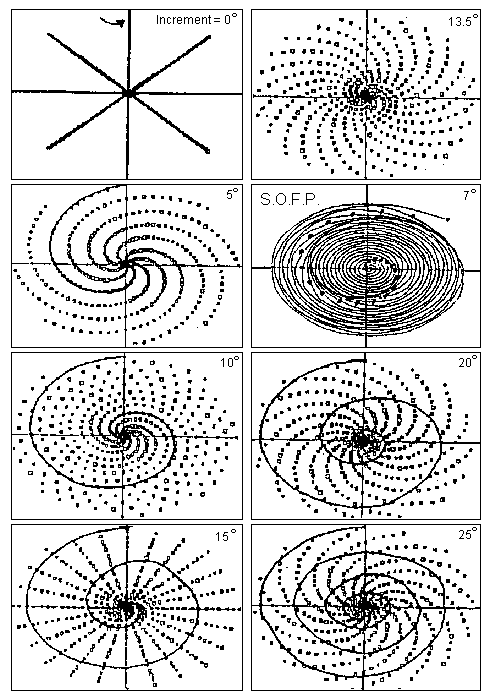
What interests me is how the m = 3, n = 8 of the leaves becomes the m = ? n = ? of the seedhead! After all, the seedhead is just a greatly shortened stem. Therefore the xylem vessels which are arranged vertically and connect every eighth leaf must be tightly twisted in the seedhead, but cannot be too twisted or scrambled. But how does the plant achieve this? No one knows! In the third figure I constructed a seedhead by making each of the eight ranks (of leaves) twist slightly (by an increment) as the head is formed. As can be seen an increment of 13.5° gives the correct pattern of spirals, including the break in the spirals in the middle of the head. However, the model is incomplete: the number of seeds in the outer spiral is 32: not a Fibonacci number. And the number of clockwise spirals equals the number of counter-clockwise spirals: this does not occur in nature. But then, I have not yet attempted to fit the spirals into the minimum space: note the large gaps between the seeds in the outer spirals. Alas, this means that I have to rewrite my computer programme, so that I cannot finish my story in this issue!
The conversion of 8 ranked leaves into a compact seedhead of 400 fruit in Protea. Seeds are illustrated with = and one of the eight xylem vessels with a solid spiral. SOFP shows the sequence in which florets are laid down (half the spirals are omitted).
Back Protea Ecology